제가 원래 이 주제 관련 탐구를 3월 말에 처음 시작해서
4~5월에 다 끝내고,
최근에 보고서도 다 작성하고
이제야 블로그에 글을 쓰네요...ㅜㅜ
참 어렵게 여기까지 온 것 같네요
일단 제가 한 탐구 내용을 소개해드리자면,
제목처럼 오차랑 상관관계를 비료하는 것인데요.
중학교 때 아마도 처음 1/2m*v^2라는 공식을 배울 겁니다.
그런데, 고등학교 물리학 1을 배우다 보면,
'질량 에너지 동등성'이라는 부분을 배울 때가 있을 텐데,
이때에는 우리가 전에 배웠던 p=m*v라는
운동량 공식이 다른 속도의 관성계에서는 성립하지 않게 됩니다.
그래서
p= γ*m0*v
라는 공식이 나오게 되죠
(이때, γ= 1/(1-(v^2/c^2))*(-1/2)입니다.)
그러면 여기서 m0*γ는 m이니까
m= m0*γ
이 성립하게 됩니다.
그러면, 이 공식을 기반으로 에너지를 나타내는 공식인
E=m*c^2
이
E = γ*m0*c^2
로 바뀌게 되는 겁니다!
그러면, E = γ*m0*c^2 가
γ=1, v=0
v=0 일 때의 에너지 이므로 m0*c^2는
물체가 가지는 '질량의 에너지(정지에너지)'라고 할 수 있겠습니다.
이때
E = γ*m0*c^2= (γ-1) m0*c^2+ m0*c^2
이고, m0*c^2 는 질량의 에너지 부분이니까,
(γ-1) m0*c^2 가 물체가 가지는 '운동에너지'라고 할 수 있겠네요.
그런데
1/2m*v^2가 (γ-1) m0*c^2 랑 같다는 게 이해가 잘 안 될 수도 있는데
γ는 분모에 v^2/c^2 부분이 나오죠
이때, v가 10m/s이면, v^2/c^2는
1.1126500560536184e-15
라는 어마무시하게 작은 수를 가지게 됩니다.
그렇다면, v가 0에 엄청 가까울 때에는
Ek ≈ 1/2mv^2
라고 볼 수 있는 겁니다.
그러니까 우리는 여태껏 물체의 운동에너지를 근삿값으로 구했던 것이죠.
여기서
"이 두 에너지 간의 오차는 과연 몇 J이나 될까?"
라는 호기심에서 제 탐구 주제가 나오게 됩니다.
일단 저는 탐구 시작 전에
"오차는 속도가 커질수록 가파르게 증가할 것이다."
라는 가설을 세웠습니다.

이 그래프를 본다면, 두 에너지 간의 오차가 가파르게 증가하는 양상을
나타내고 있어서 그렇게 유추하였습니다.

저는 위와 같은 코드로 google colab에서 두 에너지의 값을 구하고
그 오차를 획득하는 식으로 계산하였습니다.

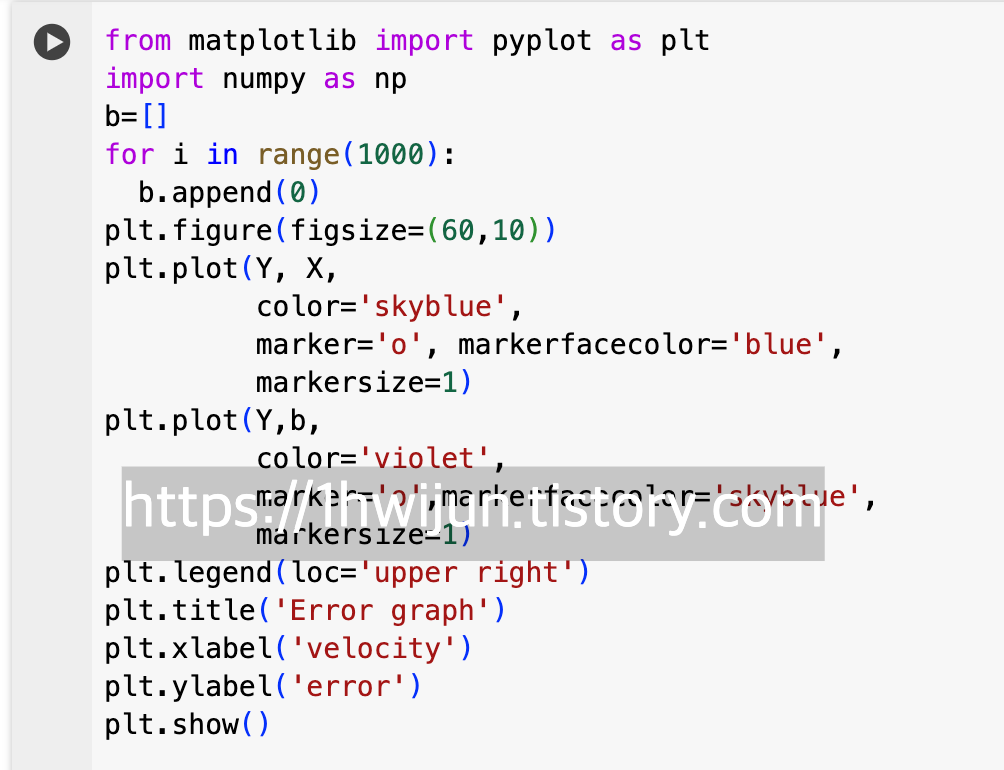
여기서는 그래프를 그리기 위해서 각 오차와 속도들을 리스트에 담아서
그래프를 그렸습니다.
그렇게 해서 그래프를 그리면

전체적으로 봤을 때, 제가 처음 세운 가설과 맞아 들어가는 것으로 보입니다.
하지만, 특정 구간을 확대하여 보게 된다면,
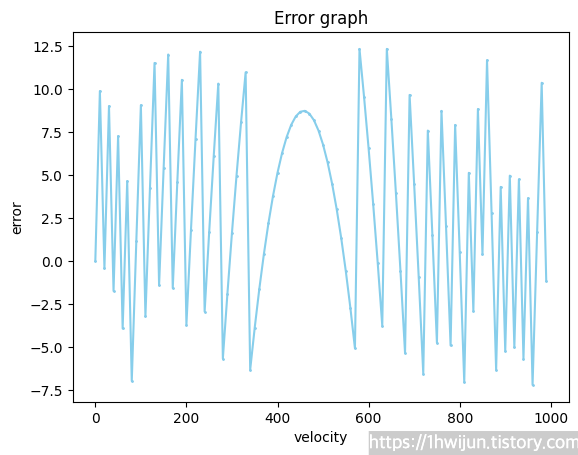
그래프가 이런 모양을 띄는데 많이 무서워ㅎㄷㄷ
괴랄하게 생겼습니다.
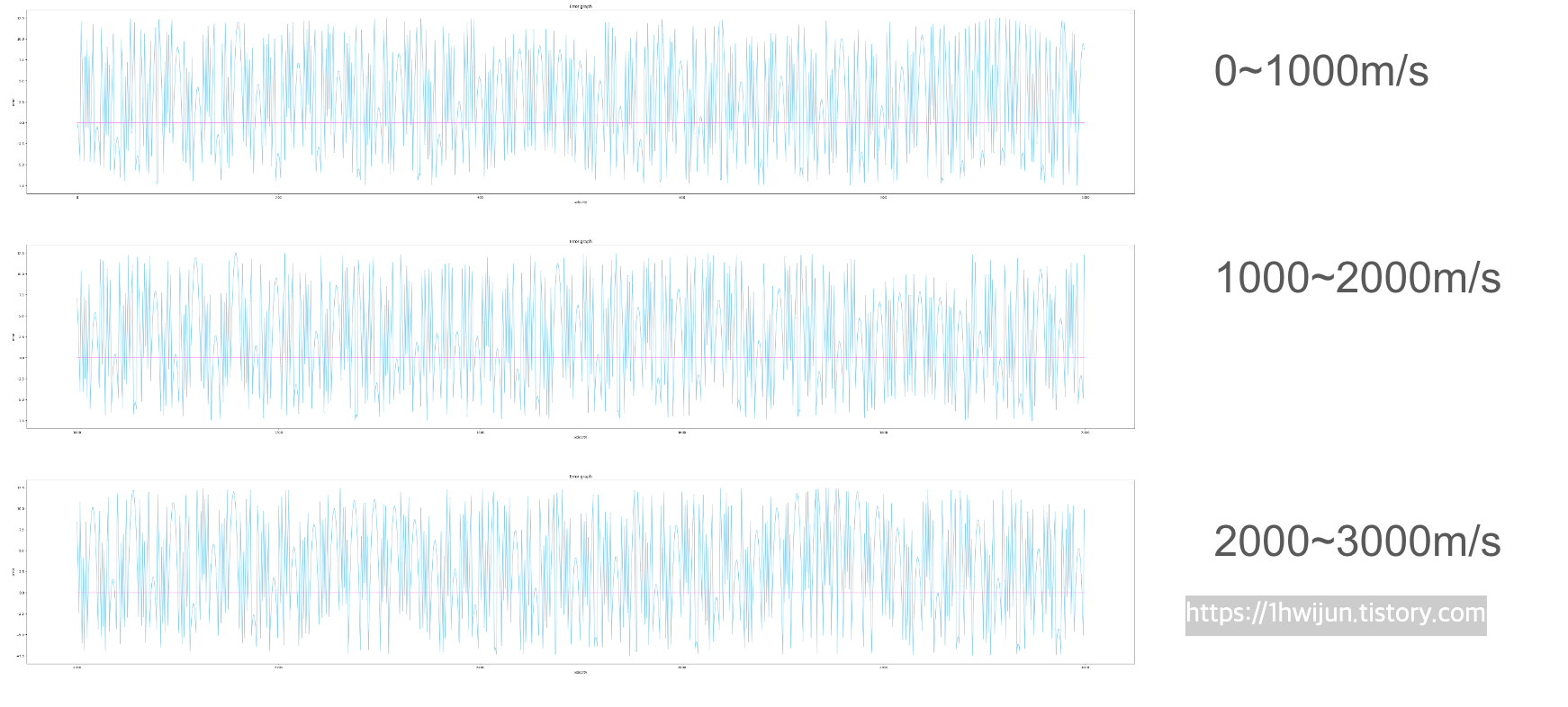
이제 각 구간을 1000m/s로 설정하고 구간별로 간격을 1로 잡아 그 그래프를 그렸습니다.
참 독특해요..
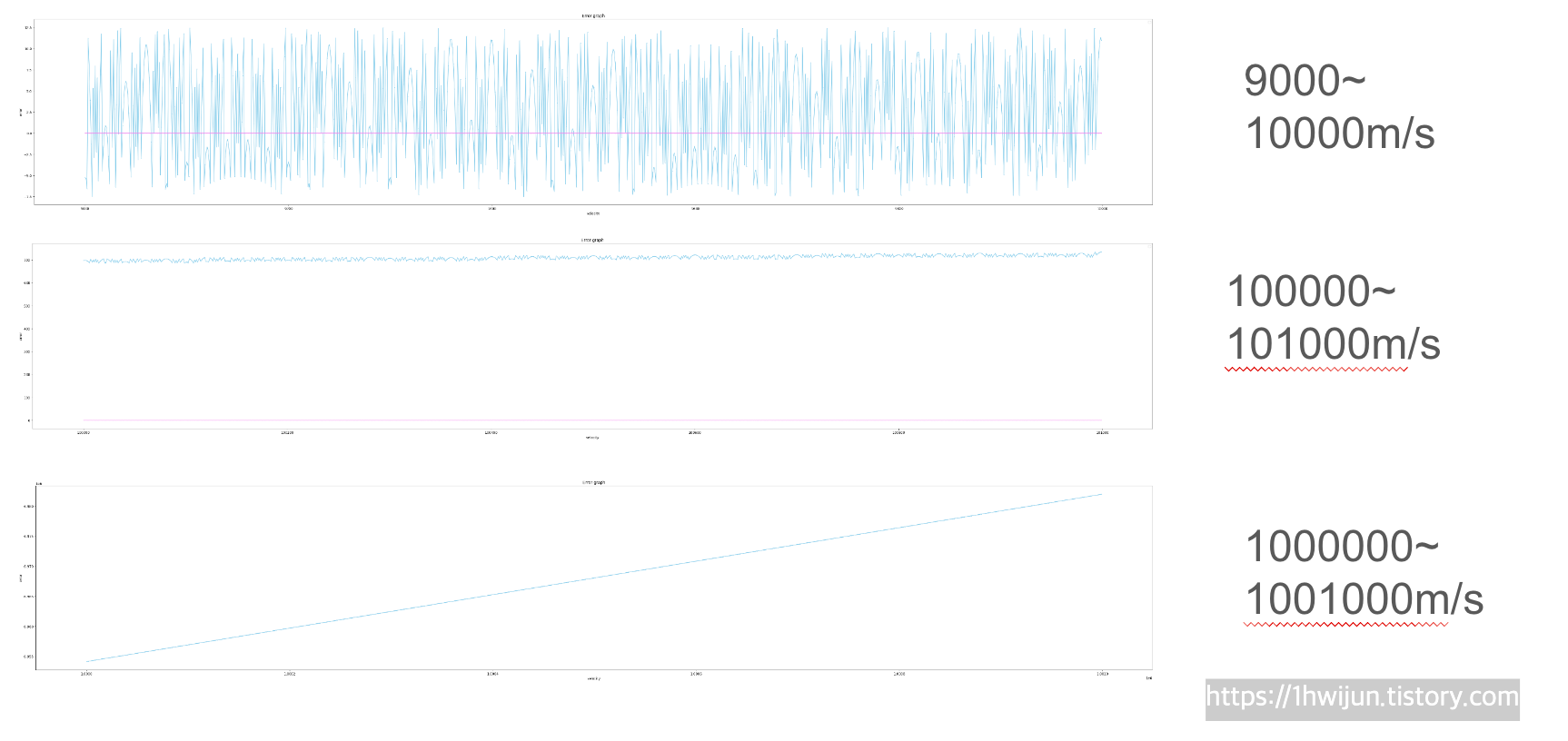
그래프가 어째서 이런 양상을 띠는지는 의문입니다.ㅜㅜ
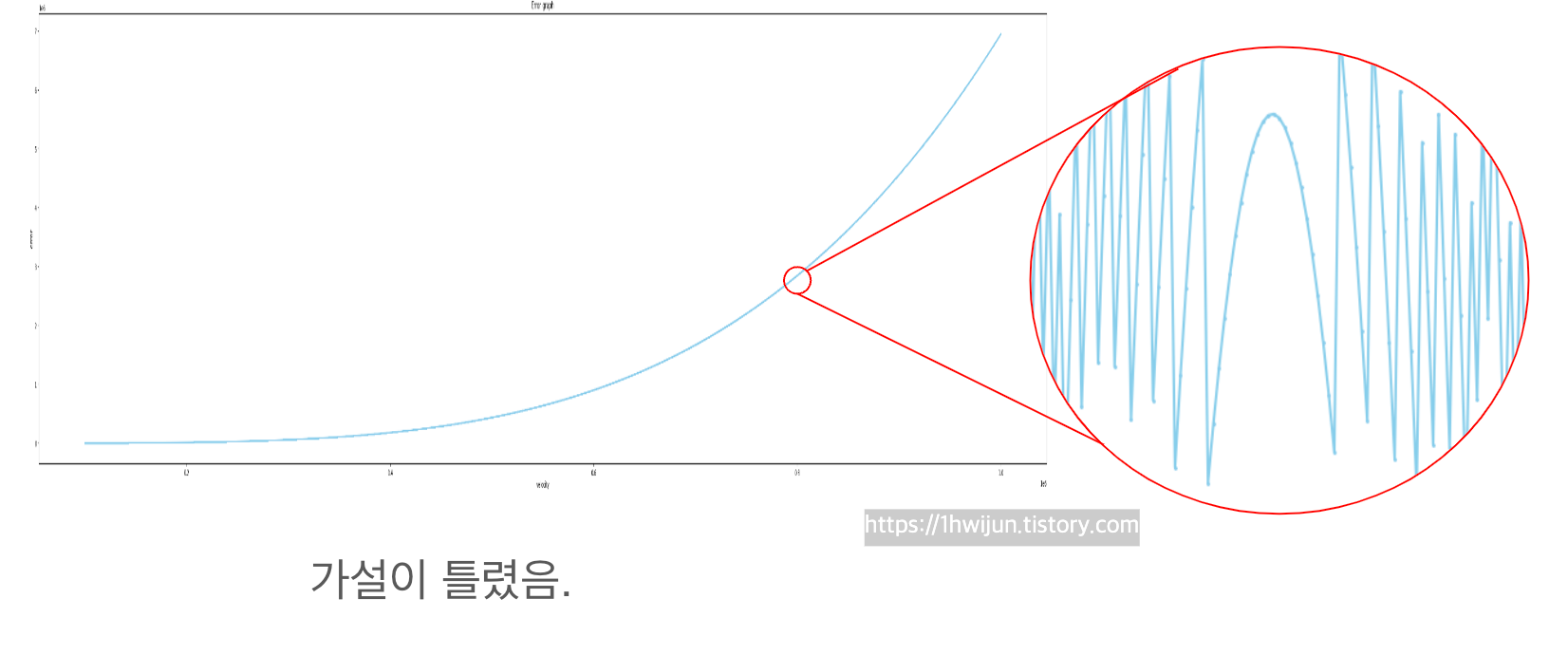
거시적으로는 제 가설이 맞는 것으로 보이지만, 미시적으로 보면
전혀 예측이 불가한 모습을 띄고 있습니다....
일단 여기까지가 제가 탐구한 내용인데,,,
이러한 현상의 원인 규명은 다음에 시간이 남다면 하도록 하겠습니다.
그럼 다음에봐용~^^